正六面体 → 正六角形
状態:-
閲覧数:3,997
投稿日:2016-05-28
更新日:2016-06-18
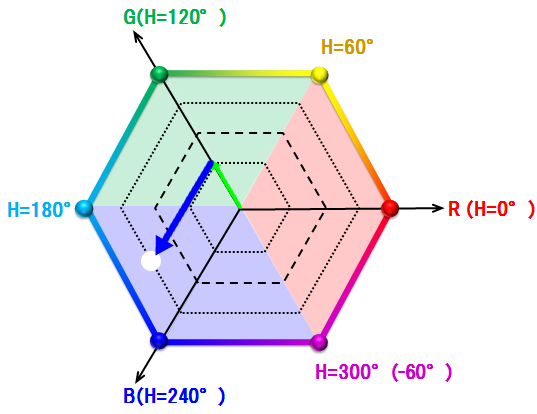
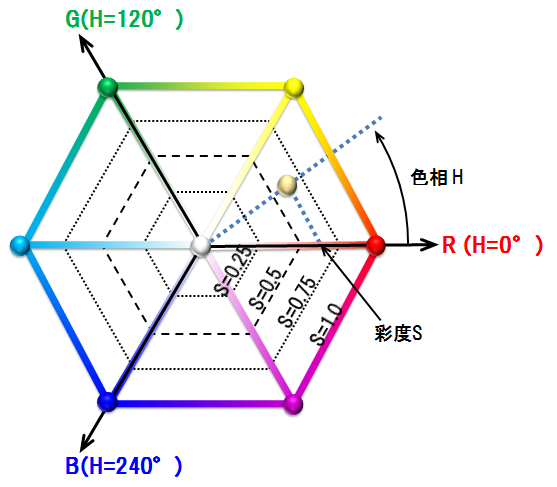
「正六面体で構成されるRGB」を、「HSL水平断面図である正六角形」へ再構成
比較一覧表
比較一覧表
| - | RGB | HSL断面図 |
|---|---|---|
| モデル | 正六面体 | 正六角形 |
| 頂点数 | 8 | 6 |
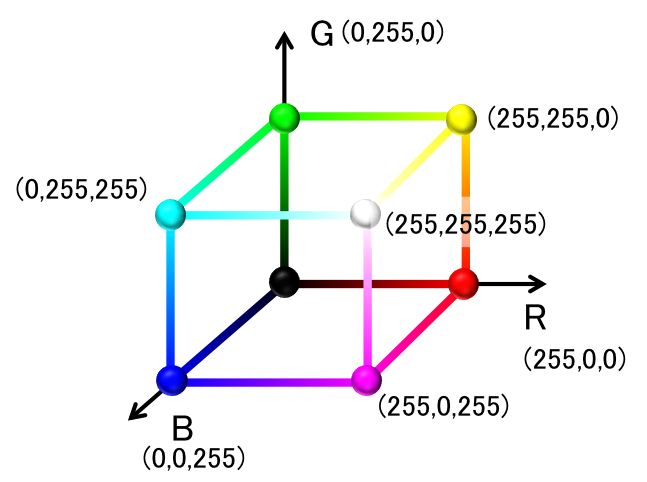
正六面体RGB
「正六面体で構成されるRGB」を、「HSL水平断面図である正六角形」へ再構成
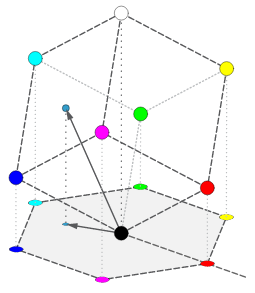
黒(0,0,0)
白(255,255,255)
・六角形の中心へ
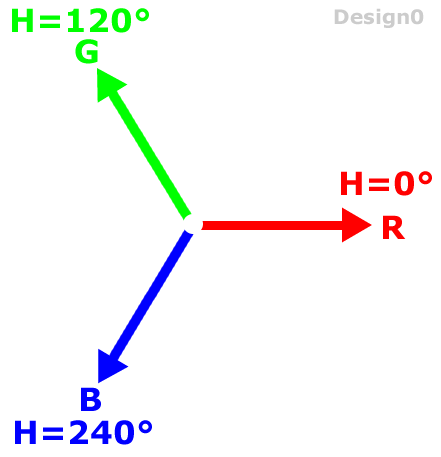
Red(255,0,0)
・H=0°へ
Green(0,255,0)
・H=120°へ
Blue(0,0,255)
・H=240°へ
イエロー(255,255,0)
・H=60°へ
シアン(0,255,255)
・H=180°へ
ピンク(255,0,255)
・H=300°へ
| H | 色 | R | G | B |
|---|---|---|---|---|
| 0° | Red | 255 | 0 | 0 |
| 60° | イエロー | 255 | 255 | 0 |
| 120° | Green | 0 | 255 | 0 |
| 180° | シアン | 0 | 255 | 255 |
| 240° | Blue | 0 | 0 | 255 |
| 300° | ピンク | 255 | 0 | 255 |
RGB各成分が最大値となるのは?
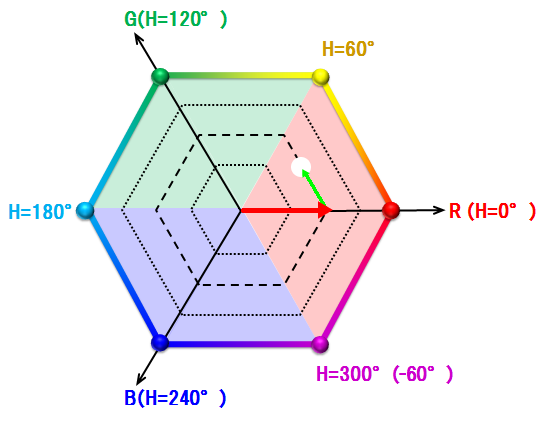
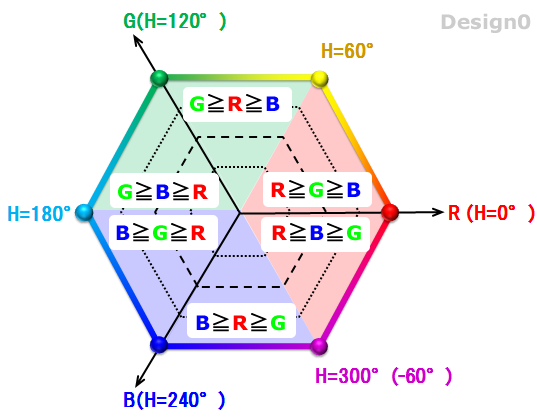
「HSL水平断面図である正六角形」をRGB各成分の大小関係で6エリアへ分類
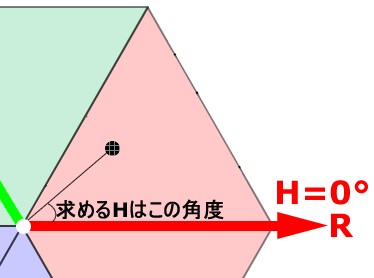
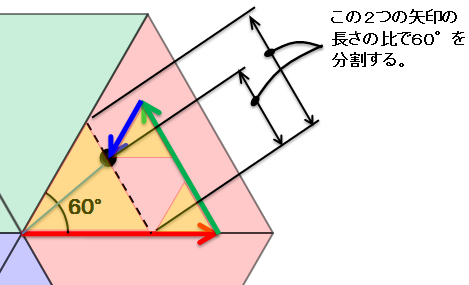
考え方A.長さの比率で角度60°を分割 / R≧G≧B
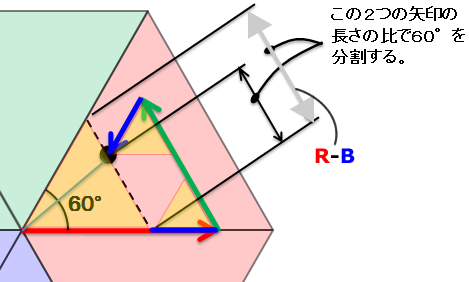
考え方A.長さの比率で角度60°を分割 / R≧B≧G
R≧B≧G
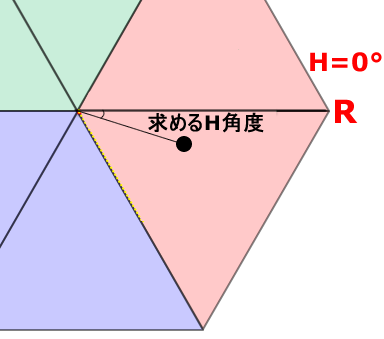
補助線(与えられた図形にはないが証明のために便宜的に線を描き加える)
→ 三辺の長さが等しい正三角形(黄色い正三角形)
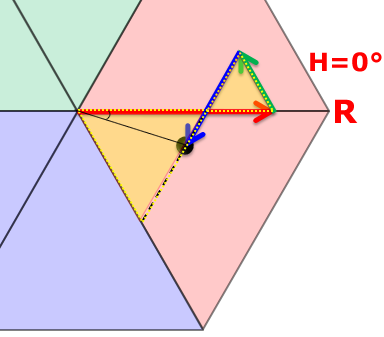
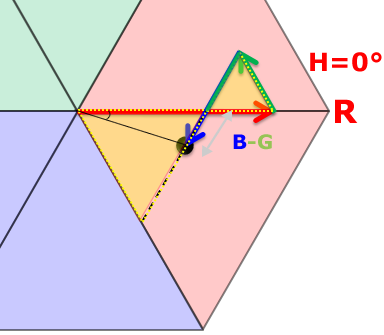
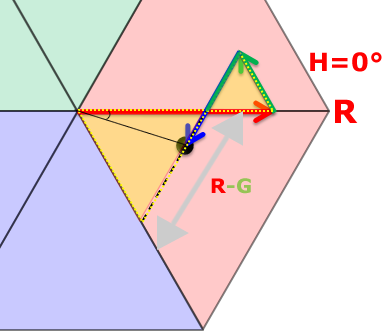
R≧B≧Gでは?
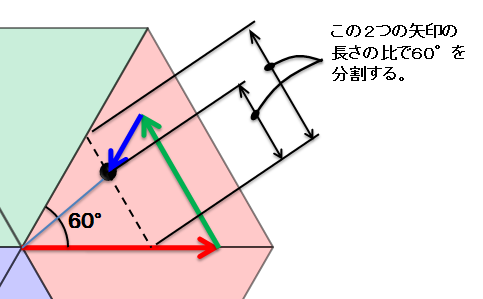
60 × (角度分の長さ ÷ 60°分の長さ)
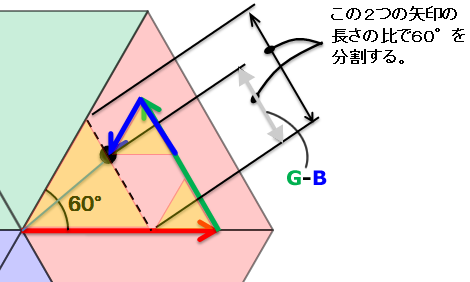
60 × ((B - G) ÷ (R - G))
Rが最大値のときで統一させるためには?
・「R≧B≧G」を「R≧G≧B」へ合わせればよい
(B - G) → (G - B)
60 × ((G - B) ÷ (R - G))+ 360
・円周状の空間の位置だから、マイナスになっても360°足してプラスにできる結論
Rが最大値のとき
60 × ((G - B) ÷ (MAX - MIN))
※結果がマイナスとなる場合は+360エリア毎の計算式 / 最大値基準
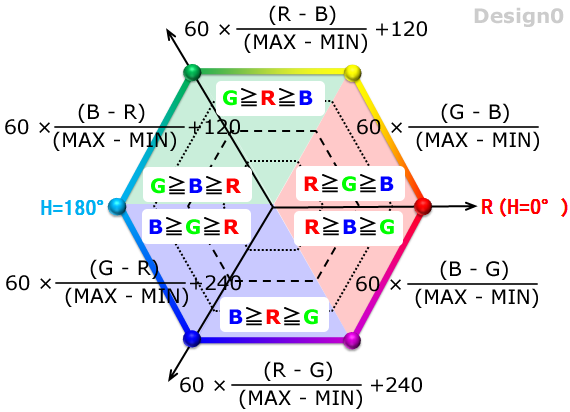
R・G・Bのうち、最も大きな値をMAX、最も小さな値をMIN
Rが最大値の場合
色相 H = 60 × ((G - B) ÷ (MAX - MIN))
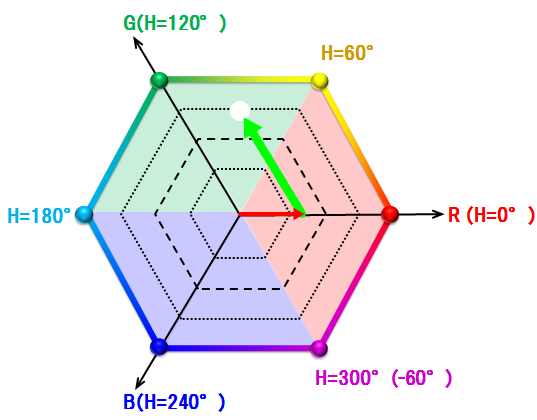
Gが最大値の場合
色相 H = 60 × ((B - R) ÷ (MAX - MIN)) +120°
Bが最大値の場合
色相 H = 60 × ((R - G) ÷ (MAX - MIN)) +240°
3つとも同じ値の場合
色相 H = 0
求められた色相がマイナス値だった場合
・360を加算して0~360の範囲に収める
・色相、彩度、明度の計算方法